Some Geometric Primitives:
Computing the area of a triangle:
Using Vector:
Let vectors AB and AC point respectively from A to B and from A to C. The area of parallelogram ABDC is then,
|AB x AC|
which is the magnitude of the cross product of vectors AB and AC. The area of triangle ABC is half of this,
0.5* |AB x AC|
Here AB x AC = |AB||AC| sinθ, so θ determine that angle between AB and AC.
Now you see, point A to B, then point C is to the left of AB (see Fig. (a) . Point C is to the right of AB (see Fig. (b). so, we can say,
For fig. a, AB x AC = |AB||AC| sinθ (positive value)
For fig. a, AB x AC = |AB||AC| sinθ (negative value)
Positive value represents that point C is to the left of AB, negative value represents that point C is to the right of AB.
Let, A(x1,y1), B = (x2,y2) and C(x3,y3).
If O is the origin of the system, then OA = x1i + y1j, (i and j are two unite vector of x and y axis). Similarly OB = x2i+y2j, OC = x3i+y3j.
AB = AO+OB = OB-OA = (x2-x1)i + (y2-y1)j
AC = AO+OC = OC-OA = (x3-x1)i + (y3-y1)j
|AB x AC|= (x2-x1)(y3-y1) –(x3-x1)(y2-y1)
The area of ABC triangle,
0.5* |AB x AC|= 0.5*(x2-x1)(y3-y1) –(x3-x1)(y2-y1)
Using coordinates:
The area of ABC triangle,
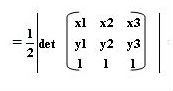
= ½*(x2y3-x3y2 – x1y3+x3y1+x1y2-x2y1)
= ½*((x2-x1)(y3-y1)-(x3-x1)(y2-y1)).
Q1. Let there are two point p1 and p2. Now draw a line through p1 and p2. If we have a point q, we will determine that q is to the left or right of p1p2 line.
Example:
See the above figure, first determine the location of point q(8,-1) respect to p1p2 line.
Let p1(x1,y1) = p1(2,-2), p2(x2,y2)=(6,3), q(x3,y3) =( 8,-1)
The area of triangle p1p2q, = ½* ((6-2)(-1+2) –(8-2)(3+2)) = ½*(4-30) = -13
So q(8,-1) is to the right of the line p1p2.
Now determine the location of point q(1,-1) respect to p1p2 line.
The area of triangle p1p2q, = ½* ((6-2)(-1+2) –(1-2)(3+2)) = ½*(4+5) = 9
So q(1,-1) is to the left of the line p1p2.
Implementation:
1) Normal C++ File:
2) Turbo C++(graphical Environment)
Next Topic:
Computing the area of a triangle:
Using Vector:
|AB x AC|
which is the magnitude of the cross product of vectors AB and AC. The area of triangle ABC is half of this,
0.5* |AB x AC|
Here AB x AC = |AB||AC| sinθ, so θ determine that angle between AB and AC.
Now you see, point A to B, then point C is to the left of AB (see Fig. (a) . Point C is to the right of AB (see Fig. (b). so, we can say,
For fig. a, AB x AC = |AB||AC| sinθ (positive value)
For fig. a, AB x AC = |AB||AC| sinθ (negative value)
Positive value represents that point C is to the left of AB, negative value represents that point C is to the right of AB.
Let, A(x1,y1), B = (x2,y2) and C(x3,y3).
If O is the origin of the system, then OA = x1i + y1j, (i and j are two unite vector of x and y axis). Similarly OB = x2i+y2j, OC = x3i+y3j.
AB = AO+OB = OB-OA = (x2-x1)i + (y2-y1)j
AC = AO+OC = OC-OA = (x3-x1)i + (y3-y1)j
|AB x AC|= (x2-x1)(y3-y1) –(x3-x1)(y2-y1)
The area of ABC triangle,
0.5* |AB x AC|= 0.5*(x2-x1)(y3-y1) –(x3-x1)(y2-y1)
Using coordinates:
The area of ABC triangle,
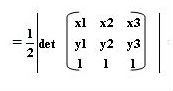
= ½*(x2y3-x3y2 – x1y3+x3y1+x1y2-x2y1)
= ½*((x2-x1)(y3-y1)-(x3-x1)(y2-y1)).
Q1. Let there are two point p1 and p2. Now draw a line through p1 and p2. If we have a point q, we will determine that q is to the left or right of p1p2 line.
Example:
See the above figure, first determine the location of point q(8,-1) respect to p1p2 line.
Let p1(x1,y1) = p1(2,-2), p2(x2,y2)=(6,3), q(x3,y3) =( 8,-1)
The area of triangle p1p2q, = ½* ((6-2)(-1+2) –(8-2)(3+2)) = ½*(4-30) = -13
So q(8,-1) is to the right of the line p1p2.
Now determine the location of point q(1,-1) respect to p1p2 line.
The area of triangle p1p2q, = ½* ((6-2)(-1+2) –(1-2)(3+2)) = ½*(4+5) = 9
So q(1,-1) is to the left of the line p1p2.
Implementation:
1) Normal C++ File:
2) Turbo C++(graphical Environment)
Next Topic:
No comments:
Post a Comment